На рисунке изображён график функции, к которому проведены касательные в четырёх точках.
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
А) K
Б) L
В) M
Г) N
1) −4
2) 3
3) 
4) −0,5
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
На рисунке изображён график функции y = f(x). Числа a, b, c, d и e задают на оси x четыре интервала. Пользуясь графиком, поставьте в cоответствие каждому интервалу характеристику функции или её производной.
А) (a; b)
Б) (b; c)
В) (c; d)
Г) (d; e)
1) производная отрицательна на всём интервале
2) производная положительна в начале интервала и отрицательна в конце интервала
3) функция отрицательна в начале интервала и положительна в конце интервала
4) производная положительна на всём интервале
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
На рисунке изображён график функции y = f( x) . Точки a, b, c, d и e задают на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной.
А) ( a; b)
Б) ( b; c)
В) ( c; d)
Г) ( d; e)
1) значения функции положительны в каждой точке интервала.
2) значения производной функции положительны в каждой точке интервала.
3) значения функции отрицательны в каждой точке интервала.
4) значения производной функции отрицательны в каждой точке интервала.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Установите соответствие между графиками линейных функций и угловыми коэффициентами прямых.
ГРАФИКИ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
1) 
2) 
3) 
4) 1
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г |
На рисунках изображены графики функций вида 
Установите соответствие между графиками функций и знаками коэффициентов a и c.
ФУНКЦИИ
КОЭФФИЦИЕНТЫ
1) 
2) 
3) 
4) 
В таблице под каждой буквой укажите соответствующий номер.
| A | Б | В | Г |
На рисунках изображены графики функций вида 
Установите соответствие между графиками функций и знаками коэффициентов k и b.
ФУНКЦИИ
КОЭФФИЦИЕНТЫ
1) 
2) 
3) 
4) 
В таблице под каждой буквой укажите соответствующий номер.
| A | Б | В | Г |
Установите соответствие между графиками функций и характеристиками этих функций на отрезке
ГРАФИКИ
ХАРАКТЕРИСТИКИ
1) функция принимает отрицательное значение в каждой точке отрезка
2) функция возрастает на отрезке
3) функция принимает положительное значение в каждой точке отрезка
4) функция убывает на отрезке
В таблице под каждой буквой укажите соответствующий номер.
| A | Б | В | Г |
На рисунках изображены графики функций и касательные, проведённые к ним в точках с абсциссой x0. Установите соответствие между графиками функций и значениями производной этих функций в точке x0.
ГРАФИКИ
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) 
2) 
3) 
4) 
В таблице под каждой буквой укажите соответствующий номер.
| A | Б | В | Г |
Установите соответствие между функциями и характеристиками этих функций на отрезке [1; 7].
А) 
Б) 
В) 
Г) 
1) функция имеет точку максимума на отрезке
2) функция убывает на отрезке
3) функция имеет точку минимума на отрезке
4) функция возрастает на отрезке
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
На рисунках изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и значениями их производной в точке x = 1.
ГРАФИКИ
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) 0,75
2) −0,2
3) 3
4) −5
Установите соответствие между графиками функций и графиками их производных.
ГРАФИКИ ФУНКЦИЙ
ГРАФИКИ ПРОИЗВОДНЫХ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Установите соответствие между формулами, которые задают функции, и характеристиками этих функций.
1) функция возрастающая
2) функция имеет точку минимума
3) функция убывающая
4) функция имеет точку максимума
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
Установите соответствие между графиками функций и графиками их производных.
ГРАФИКИ ФУНКЦИЙ
ГРАФИКИ ПРОИЗВОДНЫХ
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Установите соответствие между графиками функций и характеристиками этих функций
ГРАФИКИ ФУНКЦИЙ
ХАРАКТЕРИСТИКИ
1) на
2) на
3) на
4) на
В таблице под каждой буквой укажите соответствующий номер.
| A | Б | В | Г |
то при k > 0 функция возрастает, при k < 0 — убывает. При этом, чем больше коэффициент k по модулю, тем круче наклон графика. Следовательно, графики А и Б соответствуют отрицательным значениям k, при этом для графика А значение k должно быть больше по модулю, чем для графика Б. Значит, имеем: A — 2, Б — 3. Графики В и Г соответствуют положительным значениям k, при этом для 
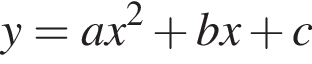— квадратичная функция, график которой — парабола. Если a > 0, то ветви параболы направлены вверх, если a < 0, то ветви параболы направлены вниз. Если c > 0, то парабола пересекает ось Oy выше оси Ox, если c < 0, то парабола пересекает Oy ниже оси Ox. 
Следовательно, производная этого графика в точке 
должна менять свой знак с отрицательного на положительный. Данный график производной указан под цифрой 4.
Следовательно, производная этого графика в точке 
должна менять свой знак с отрицательного на положительный. Данный график производной указан под цифрой 1.
Следовательно, производная этого графика в точке 
должна менять свой знак с положительного на отрицательный. Данный график производной указан под цифрой 3.
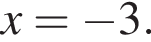Следовательно, производная этого графика в точке 
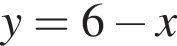
задает уравнение квадратичной функции, график которой — парабола с вершиной (2; 3), ветви которой направлены вверх. Значит, точка (2; 3) является точкой минимума.
Следовательно, производная этого графика в точке 
должна менять свой знак с отрицательного на положительный. Данный график производной указан под цифрой 2.
Следовательно, производная этого графика в точке 
Следовательно, производная этого графика в точке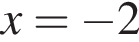 
должна менять свой знак с положительного на отрицательный. Данный график производной указан под цифрой 3.