Варианты заданий
Версия для печати и копирования в MS Word1
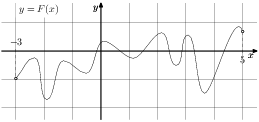
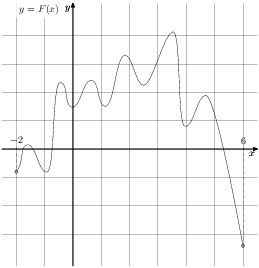
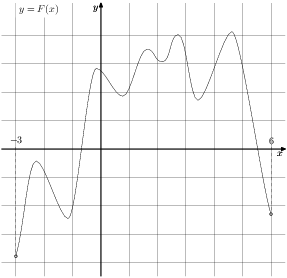
На рисунке изображён график функции y = F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52




 На рисунке изображён график функции
На рисунке изображён график функции 


 — одной из первообразных некоторой функции
— одной из первообразных некоторой функции  , определённой на интервале
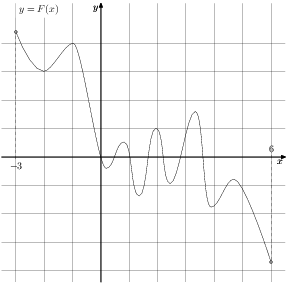
, определённой на интервале  . Пользуясь рисунком, определите количество решений уравнения
. Пользуясь рисунком, определите количество решений уравнения  на отрезке
на отрезке ![[-1;3]](/fbms/63/cc/63/55/63cc6355441f0466f7aa34193d1f067b.png) .
.
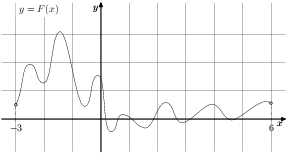
 . Пользуясь рисунком, определите количество решений уравнения
. Пользуясь рисунком, определите количество решений уравнения ![[-1;5]](/fbms/c4/b2/fe/25/c4b2fe25d854abc71dc9ebdb59a73d4c.png) .
.
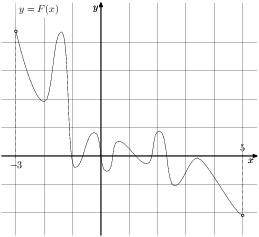
 . Пользуясь рисунком, определите количество решений уравнения
. Пользуясь рисунком, определите количество решений уравнения ![[-2;4]](/fbms/aa/a4/52/e9/aaa452e90f9de43f86281bba800ca1f6.png) .
.

 . Пользуясь рисунком, определите количество решений уравнения
. Пользуясь рисунком, определите количество решений уравнения ![[-2;3]](/fbms/a3/83/a1/30/a383a1308affb93d5d3a380dd90d7977.png) .
.

 . Пользуясь рисунком, определите количество решений уравнения
. Пользуясь рисунком, определите количество решений уравнения ![[-1;4]](/fbms/0d/78/cb/2c/0d78cb2c75e4bc4b12f841e3bb65263a.png) .
.



 . Пользуясь рисунком, определите количество решений уравнения
. Пользуясь рисунком, определите количество решений уравнения ![[-2;5]](/fbms/0a/da/0d/e2/0ada0de25d494cd1b6f4fe46362c226e.png) .
.