1. Тип Д18 № 245173 

Наибольшее и наименьшее значение функций. Исследование функций без помощи производной
i
Найдите точку максимума функции 
Решение. Квадратный трехчлен 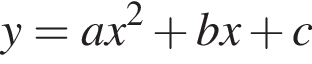 с отрицательным старшим коэффициентом достигает максимума в точке
с отрицательным старшим коэффициентом достигает максимума в точке 
 возрастающая, а заданная функция определена при найденном значении переменной, она достигает максимума в той же точке, в которой достигает максимума подкоренное выражение.
возрастающая, а заданная функция определена при найденном значении переменной, она достигает максимума в той же точке, в которой достигает максимума подкоренное выражение.
Ответ: −2.
Ответ: -2
245173
-2





 в нашем случае — в точке 3, и оно равно 4. Следовательно, наименьшее значение заданной функции
в нашем случае — в точке 3, и оно равно 4. Следовательно, наименьшее значение заданной функции 

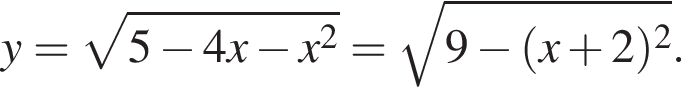
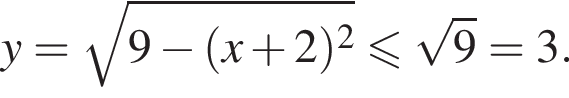
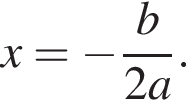 В нашем случае наибольшее значение достигается в точке −2 и равно 9. Поскольку функция
В нашем случае наибольшее значение достигается в точке −2 и равно 9. Поскольку функция 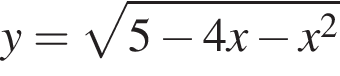 имеем:
имеем: 

 возрастает и функция
возрастает и функция  определена в точке 1, она также достигает в ней максимума.
определена в точке 1, она также достигает в ней максимума.
 возрастает и заданная функция
возрастает и заданная функция 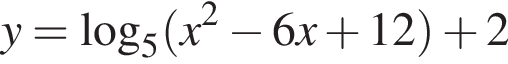 определена в точке 3, она также достигает в ней минимума.
определена в точке 3, она также достигает в ней минимума. 
 в этой точке определена и принимает значение
в этой точке определена и принимает значение  Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции.
Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции.

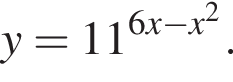
 возрастающая, заданная функция достигает максимума в той же точке, в которой достигает максимума выражение
возрастающая, заданная функция достигает максимума в той же точке, в которой достигает максимума выражение  Квадратный трехчлен
Квадратный трехчлен 
 Квадратный трехчлен
Квадратный трехчлен 
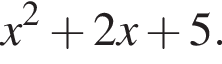 Квадратный трехчлен
Квадратный трехчлен 

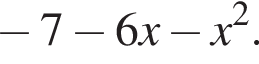 Квадратный трехчлен
Квадратный трехчлен 