Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч 2, вычисляется по формуле  Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону 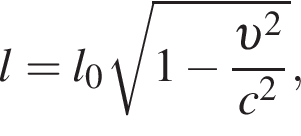 где l0 = 5 м — длина покоящейся ракеты, c = 3 · 105 км/с — скорость света, а υ — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с.
где l0 = 5 м — длина покоящейся ракеты, c = 3 · 105 км/с — скорость света, а υ — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с.
Расстояние от наблюдателя, находящегося на небольшой высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле  где
где  км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 4 километров? Ответ выразите в метрах.
км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 4 километров? Ответ выразите в метрах.
Расстояние (в км) от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле  где
где  км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?
км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?
Расстояние (в км) от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле  где
где  км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
Расстояние (в км) от наблюдателя, находящегося на небольшой высоте h километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле  где
где  (км)
(км)
Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле  где
где  — радиус Земли. С какой высоты горизонт виден на расстоянии 160 километров? Ответ выразите в километрах.
— радиус Земли. С какой высоты горизонт виден на расстоянии 160 километров? Ответ выразите в километрах.
Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле  где
где  — радиус Земли. С какой высоты горизонт виден на расстоянии 144 километров? Ответ выразите в километрах.
— радиус Земли. С какой высоты горизонт виден на расстоянии 144 километров? Ответ выразите в километрах.
Гоночный автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a км/ч2.  где l — пройденный автомобилем путь. Определите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 250 метров, приобрести скорость 60 км/ч. Ответ выразите в км/ч2.
где l — пройденный автомобилем путь. Определите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 250 метров, приобрести скорость 60 км/ч. Ответ выразите в км/ч2.

 при известном значении длины пути
при известном значении длины пути 
 при заданном значении длины покоящейся ракеты
при заданном значении длины покоящейся ракеты  и известной величине скорости света
и известной величине скорости света 
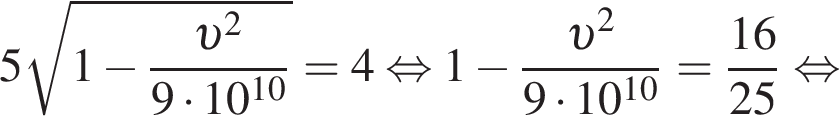



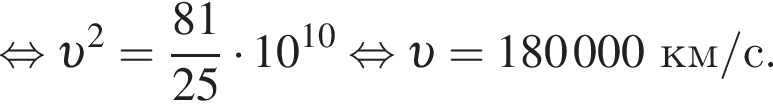






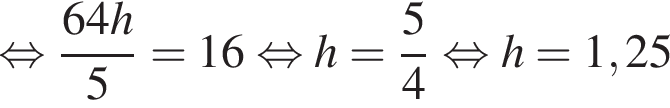
 В формуле, приведённой в задании, коэффициент 500 как раз отражает, то что все величины, за исключением h, выражены в километрах.
В формуле, приведённой в задании, коэффициент 500 как раз отражает, то что все величины, за исключением h, выражены в километрах. и
и  при заданном значении R:
при заданном значении R:

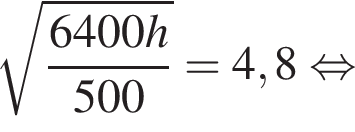


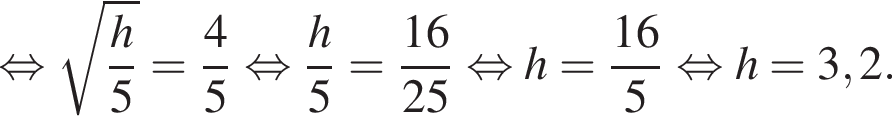


 метра.
метра.
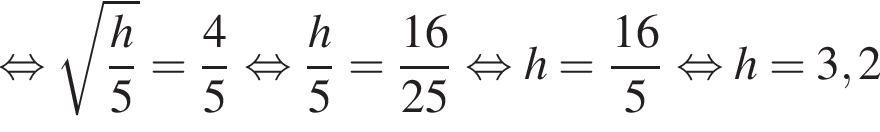
 ступенек.
ступенек.

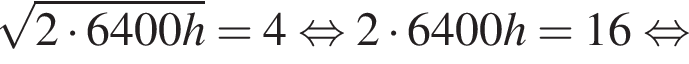

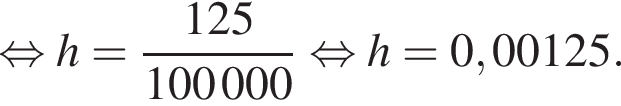




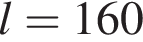 при заданном значении R:
при заданном значении R: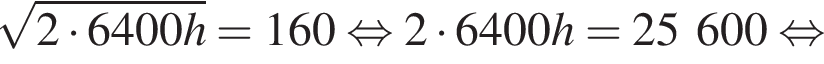



 при заданном значении R:
при заданном значении R:



