

На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
Разность значений первообразной в точках 6 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ:7.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
Разность значений первообразной в точках 8 и 4 равна площади выделенной на рисунке трапеции
Поэтому
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
Разность значений первообразной в точках 8 и 6 равна площади выделенной на рисунке трапеции Поэтому
Ответ:12.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
Решение.
Это задание ещё не решено, приводим решение прототипа.
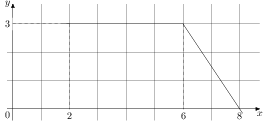
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
Решение.
Это задание ещё не решено, приводим решение прототипа.
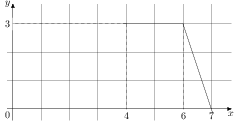
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
Решение.
Это задание ещё не решено, приводим решение прототипа.
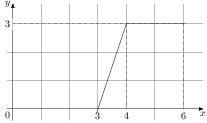
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
Решение.
Это задание ещё не решено, приводим решение прототипа.
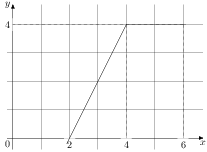
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
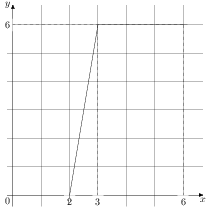
Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
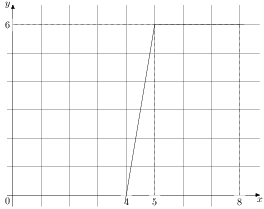
Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
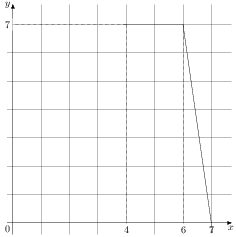
Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
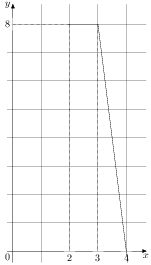
Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции
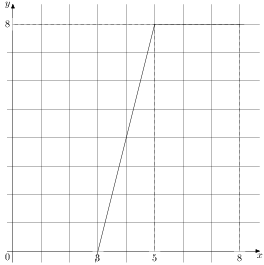
Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
где
— одна из первообразных функции

Решение.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому
Ответ: 7.
Примечание Д. Д. Гущина.
В связи с возникающими у учителей вопросами приведем аналитическое решение; излишне громоздкое для данной задачи, но раскрывающее смысл констант в записи неопределенного интеграла. Разобраться в нем будет полезно и ученикам, желающим глубже понять тему.
Пользуясь данным в условии графиком, запишем функцию в виде
Запишем выражение для первообразной:
Заметим, что первообразная является дифференцируемой, а потому и непрерывной функцией в каждой точке своей области определения. Следовательно, непрерывной в точке 3. Поэтому выражения для первообразных в точке 3 должны быть равными. Подставим в уравнение
получим:
откуда Следовательно,
Пока найдена непрерывная функция F, которая является первообразной функции f на луче и на полуинтервале
Осталось изучить дифференцируемость F в точке 3. Найдем левостороннюю и правостороннюю производные:
Левосторонняя производная F в точке 3 равна правосторонней, а потому Теперь можно утверждать, что функция F является первообразной для f на всей области определения. Для ответа на вопрос задачи осталось найти разность значений первообразной в точках
Ответ: 7.
Замечание. Отметим дополнительно, что левосторонняя и правосторонняя производные производные определяются как
Если положить в первой из этих формул а во второй —
то соответственно:
и
откуда следуют более удобные для вычислений формулы:
которые были использованы выше в решении.
Пытливый читатель мог бы заинтересоваться тем, как «склеены» между собой ветви графика найденной первообразной в точке с абсциссой 3. Говоря более формально, необходимо узнать, каков угол между касательными лучами к ветвям графика функции f, проведенными в их общей точке. Чтобы ответить на этот вопрос, рассмотрим функции и
Из приведенных выше рассуждений следует, что
и
Но система уравнений
есть условие касания графиков функций f и g в точке x0. Итак, для любого значения константы С1 прямая является касательной к параболе
Более простой способ показать касание не связан с производной. Покажем, что прямая является касательной к параболе
то есть уравнение
имеет ровно один корень, равный 3, а значит, для любого значения С эти прямая и парабола имеют единственную общую точку — точку касания.
Отметим дополнительно, что задания указанного типа должны быть знакомы учителям, например, по известной книге Галицкого М. Л., Мошковича М. М., Шварцбурда С. И. Углубленное изучение алгебры и математического анализа (Москва, 1982): см. задание 4 из интересной, кстати, и самой по себе контрольной работы для 10 (11) класса с углубленным изучением математики.
Более простая задача приводится с решением в пособии Саакяна С. М. и др. Задачи по алгебре и началам анализа для 10–11 классов: необходимо найти общий вид первообразных функции К сожалению, приведенное авторами решение (см. ниже) нельзя признать полностью удовлетворительным, поскольку в нем не проверяется дифференцируемость найденной первообразной в точке 1. Предостерегаем читателя от этой ошибки.
Из более новых работ рекомендуем обратиться к учебнику М. Я. Пратусевича и др. Алгебра и начала математического анализа, разобран полностью без упущений.
Аналоги к заданию № 323078: 323183 323273 323275 ...323183 323273 323275 323185 323187 323189 323191 323193 323195 323197 323199 323201 323203 323205 323207 323209 323211 323213 323215 323217 323219 323221 323223 323225 323227 323229 323231 323233 323235 323237 323239 323241 323243 323245 323247 323249 323251 323253 323255 323257 323259 323261 323263 323265 323267 323269 323271 323277 323279 323281 Все
Наверх

