ЕГЭ–2025, математика базовая: задания, ответы, решения

Задания

Версия для печати и копирования в MS Word

Тип Д2 № 317863 Добавить в вариант

На рисунке изображён график $y=f' левая круглая скобка x правая круглая скобка$ производной функции $f левая круглая скобка x правая круглая скобка$ и двенадцать точек на оси абсцисс: $x_1,$ $x_2,$ $x_3,$ $\dots,$ $x_12.$ В скольких из этих точек функция $f левая круглая скобка x правая круглая скобка$ убывает?

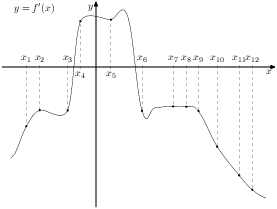
b8_2_minus_19.0.eps

Решение.

Это задание ещё не решено, приводим решение прототипа.

На рисунке изображён график $y=f' левая круглая скобка x правая круглая скобка$   — производной функции $f левая круглая скобка x правая круглая скобка$   — и восемь точек на оси абсцисс: $x_1,$ $x_2,$ $x_3,$ $\dots ,$ $x_8.$ В скольких из этих точек функция $f левая круглая скобка x правая круглая скобка$ убывает?

Убыванию дифференцируемой функции $f левая круглая скобка x правая круглая скобка$ соответствуют неположительные значения её производной. Производная неположительна в точках $x_1,x_2,x_3,x_4,x_8$ : точки лежат ниже оси абсцисс, их ординаты отрицательны. Таких точек 5.

Ответ: 5.

Прототип задания