1. Тип Д18 № 26714 

Наибольшее и наименьшее значение функций. Исследование показательных и логарифмических функций
i
Найдите наименьшее значение функции  на отрезке
на отрезке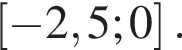
Решение. Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

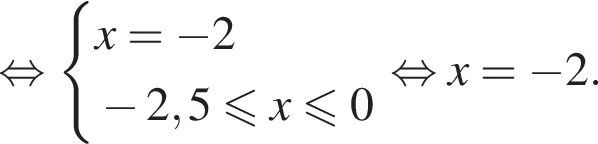


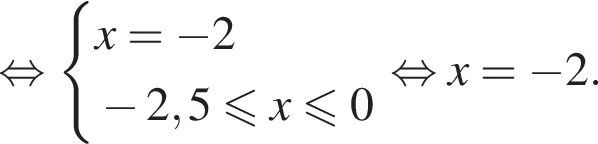




Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
В точке  заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

Ответ: −6.
Ответ: -6
26714
-6
 на отрезке
на отрезке 







 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: 
 на отрезке [−6,5; 0].
на отрезке [−6,5; 0].

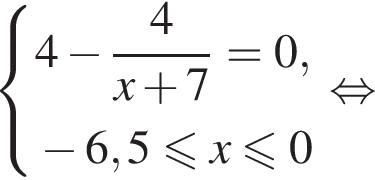



 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
 на отрезке [−6,5; 0].
на отрезке [−6,5; 0].


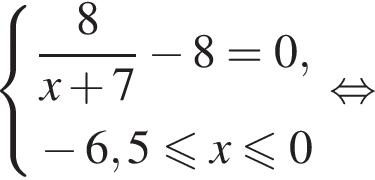



 на отрезке
на отрезке 





 на отрезке
на отрезке 




 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: 
 на отрезке
на отрезке 





 на отрезке
на отрезке 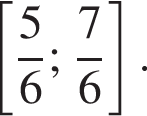



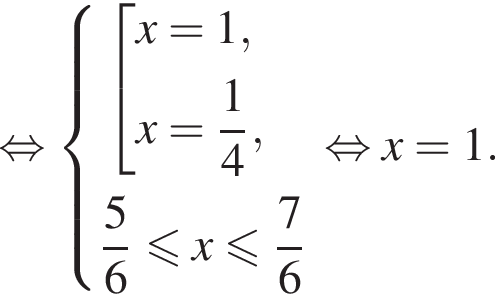


 Найдем производную заданной функции:
Найдем производную заданной функции: 








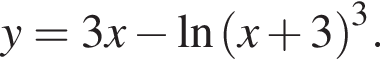
 Область определения функции — открытый луч
Область определения функции — открытый луч  Найдем производную заданной функции:
Найдем производную заданной функции: 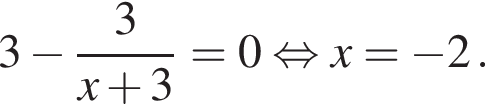





 Область определения функции — открытый луч
Область определения функции — открытый луч  Найдем производную заданной функции:
Найдем производную заданной функции: 
 Определим знаки производной функции и изобразим на рисунке поведение функции:
Определим знаки производной функции и изобразим на рисунке поведение функции: 

 Область определения функции — открытый луч
Область определения функции — открытый луч 

 Область определения функции — открытый луч
Область определения функции — открытый луч 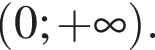 Найдем производную заданной функции:
Найдем производную заданной функции: 



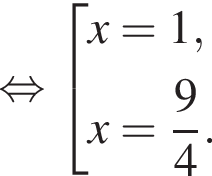
 Определим знаки производной функции и изобразим на рисунке поведение функции:
Определим знаки производной функции и изобразим на рисунке поведение функции: 





 на отрезке
на отрезке 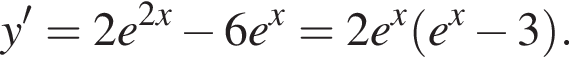





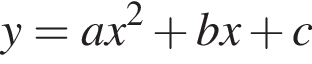 с отрицательным старшим коэффициентом достигает наибольшего значения в точке
с отрицательным старшим коэффициентом достигает наибольшего значения в точке  в нашем случае — в точке
в нашем случае — в точке  в этой точке определена. Поскольку логарифмическая функция с основанием, большим единицы, возрастает, то
в этой точке определена. Поскольку логарифмическая функция с основанием, большим единицы, возрастает, то 
 в этой точке определена и принимает значение
в этой точке определена и принимает значение  Поскольку логарифмическая функция с основанием, меньшим 1, убывает, найденное значение является искомым наибольшим значением заданной функции.
Поскольку логарифмическая функция с основанием, меньшим 1, убывает, найденное значение является искомым наибольшим значением заданной функции.
 а значит,
а значит,




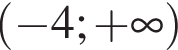 производная положительна, а функция не имеет экстремумов. На луче
производная положительна, а функция не имеет экстремумов. На луче  производная обращается в нуль в точке −5, которая является точкой максимума.
производная обращается в нуль в точке −5, которая является точкой максимума.