
Найдите наименьшее значение функции 
Решение.
Это задание ещё не решено, приводим решение прототипа.
Найдите наименьшее значение функции 
Выделим полный квадрат:

Отсюда имеем:

Поэтому наименьшее значение функции достигается в точке 3, и оно равно 2.
Ответ: 2.
Приведем другое решение.
Поскольку функция  возрастающая, а подкоренное выражение положительно при всех значениях переменной, заданная функция достигает наименьшего значения в той же точке, в которой достигает наименьшего значения подкоренное выражение. Квадратный трехчлен
возрастающая, а подкоренное выражение положительно при всех значениях переменной, заданная функция достигает наименьшего значения в той же точке, в которой достигает наименьшего значения подкоренное выражение. Квадратный трехчлен 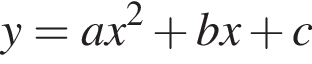 с положительным старшим коэффициентом достигает наименьшего значения в точке
с положительным старшим коэффициентом достигает наименьшего значения в точке  в нашем случае — в точке 3, и оно равно 4. Следовательно, наименьшее значение заданной функции
в нашем случае — в точке 3, и оно равно 4. Следовательно, наименьшее значение заданной функции 