Тип Д15 № 27667 
Планиметрия . Координатная плоскость
i
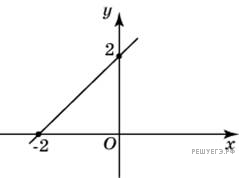Найдите угловой коэффициент прямой, проходящей через точки с координатами (−2; 0) и (0; 2).
Решение. Уравнение прямой имеет вид: y = kx + b, где k — угловой коэффициент. Подставляя координаты точек, получим систему уравнений на величины k и b :
Угловой коэффициент прямой равен 1.
Ответ: 1.
Приведем другое решение.
Прямая отсекает на координатных осях равные отрезки. Они являются катетами равнобедренного прямоугольного треугольника (см. рис.), поэтому тангенс угла наклона прямой, равный отношению противолежащего катета к прилежащему, равен 1.
Ответ: 1
PDF-версии: горизонтальная · вертикальная · крупный шрифт · с большим полем