Диаметр AB окружности с центром в точке O пересекает хорду MN этой окружности в точке H так, что MH = NH. Найдите MO, если MB = 21, HB = 15.
Решение. Отрезок MO — радиус заданной окружности. Обозначим его буквой R. Соединим отрезками точки М и N с центром окружности (см. рис.), а также с точкой А. В треугольнике MON
следовательно, треугольник MON — равнобедренный, у которого отрезок OH — медиана по условию. Но тогда отрезок OH является также высотой этого треугольника, то есть отрезок OH и диаметр AB перпендикулярны хорде MN. Тогда в треугольнике MHB по теореме Пифагора:
Угол AMB — вписанный, опирающийся на диаметр, а значит, прямой. Высота MH прямоугольного треугольника AMB, опущенная из вершины прямого угла М на гипотенузу AB, является средней пропорциональной величиной между проекциями катетов AH и BH на гипотенузу АВ. Значит,
откуда 
то есть 
Ответ: 14,7.
Другие решения.
Считая перпендикулярность AB и MN уже доказанной, приведем еще несколько способов нахождения длины отрезка MO.
Способ 2 (см. рис.). Соединим отрезком точки В и N. Исходя из соображений симметрии окружности относительно диаметра АВ, имеем:
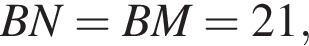
Кроме того, 
Треугольник MBN — вписанный, поэтому его площадь равна 
то есть
Замечание. Здесь использована формула для радиуса описанной окружности треугольника.
Способ 3 (см. рис.). Угол AMB — вписанный, опирающийся на диаметр, а значит, угол AMB равен 90°. В треугольнике AMB катет MB является средней пропорциональной величиной между гипотенузой AB (она же является диметром окружности) и проекцией катета МВ на гипотенузу АВ, то есть 
откуда:
Способ 4 (см. рис.). Обозначим равные углы MBO и BMO через α. Тогда 
В прямоугольном треугольнике BHM:
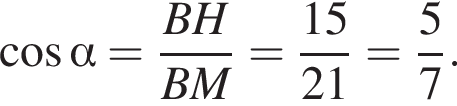
В треугольнике MOB по теореме косинусов:
то есть 
откуда
Способ 5 (см. рис.). Если угол MBA равен α, то угол MAB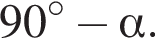 
В соответствии со следствием из теоремы синусов в треугольнике AMB получаем 
то есть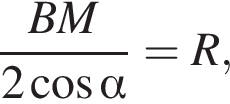 
откуда
Примечание.
Заметим, что в условии задачи нет указания на взаимное расположение точек B, O и H. Можно было бы провести хорду MN таким образом, чтобы точка H попала на отрезок OB. Однако в этом случае радиус окружности получился бы отрицательным. Следовательно, хорда MN должна быть расположена таким образом, чтобы точка H попала на отрезок OA.